\documentclass[8pt,a4paper]{report}
\usepackage{multicol}
\usepackage{amssymb}
\usepackage{xcolor}
\usepackage{tkz-tab}
\usepackage[margin=1cm]{geometry}
\usepackage{amsmath,amsfonts,amssymb,mathrsfs,tikz,eso-pic,array,colortbl}
\usepackage[most]{tcolorbox}
\def\cadre{
\begin{tikzpicture}[remember picture,overlay]
\coordinate (1) at ([shift={(-.5cm,-.5cm)}]current page.north east);
\coordinate (2) at ([shift={(.5cm,-.5cm)}]current page.north west);
\coordinate (3) at ([shift={(.5cm,.5cm)}]current page.south west);
\coordinate (4) at ([shift={(-.5cm,.5cm)}]current page.south east);
\draw[thick,col1] (1)rectangle(3);
\node[col1,fill=col1,text=white,minimum size=5mm] at (1){};
\node[col1,fill=col1,text=white,minimum size=5mm] at (2){};
\node[col1,fill=col1,text=white,minimum size=5mm] at (3){};
\node[col1,fill=col1,text=white,minimum size=5mm] at (4){};
\end{tikzpicture}
}
\colorlet{col1}{red!70}
\AddToShipoutPictureBG{\cadre}
\tcbset{box0/.style={enhanced,drop fuzzy shadow southeast=col1,boxsep=1mm,size=fbox,colback=col1!5,arc is angular,arc=2mm}}
\newtcolorbox{box0}{box0}
\newtcolorbox[auto counter]{ex}{enhanced,breakable,arc=2mm,arc is angular,drop fuzzy shadow southeast=col1,colback=col1!5,attach boxed title to top left={yshift*=-\tcboxedtitleheight/2,xshift=1cm},boxed title style={sharp corners,colback=col1!80,drop large lifted shadow=col1,right=5mm,left=5mm,colframe=col1,valign=center},title={Exercice~\thetcbcounter},fonttitle=\Large\bfseries,boxrule=1pt,colframe=col1}
\begin{document}
\begin{box0}
\renewcommand{\arraystretch}{2}
\begin{tabular}{|>{\raggedright\arraybackslash}p{.33\linewidth}|>{\centering\arraybackslash}p{0.3\linewidth}|>{\raggedright\arraybackslash}p{0.3\linewidth}|}
\arrayrulecolor{col1}
\hline
Lycée: Sebaayoune Al-jadida&\bfseries Representation des fonctions    &Niveau : deuxième bac pc 1 et 2\\\cline{1-1}\cline{3-3}
Année scolaire : 2025/2026&\bfseries &Prof : jawad loulichki\\\hline
\end{tabular}
\end{box0}
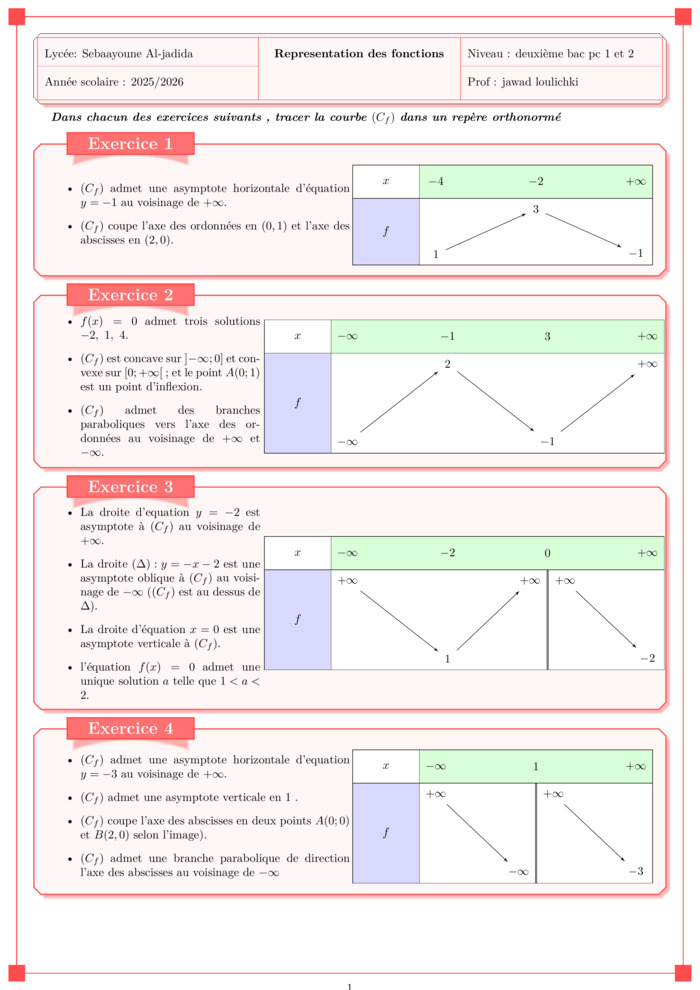
\textbf{\textit{Dans chacun des exercices suivants , tracer la courbe $(C_f)$ dans un repère orthonormé}}
\begin{ex}
\begin{minipage}[l]{0.5\linewidth}
\begin{itemize}
  \item $(C_f)$ admet une asymptote horizontale d’équation $y=-1$ au voisinage de $+\infty$.
  \item $(C_f)$ coupe l'axe des ordonnées en $(0,1)$ et l'axe des abscisses en $(2,0)$.
\end{itemize}
\end{minipage}
\begin{minipage}[r]{0.5\linewidth}
\begin{tikzpicture}
   \tkzTabInit[color, colorC = blue!15, colorL = green!15]{$x$ / 1 ,$f$ / 2}{$-4$, $-2$, $+\infty$}

   \tkzTabVar{-/$1$,+/$3$,-/$-1$}
\end{tikzpicture}
\end{minipage}
\end{ex}
\begin{ex}
\begin{minipage}[l]{0.35\linewidth}
\begin{itemize}
  \item $f(x)=0$ admet trois solutions $-2,\ 1,\ 4$.
  \item $(C_f)$ est concave sur $]-\infty;0]$ et convexe sur $[0;+\infty[$ ; et le point $A(0;1)$ est un point d'inflexion.
  \item $(C_f)$ admet des branches paraboliques vers l'axe des ordonnées au voisinage de $+\infty$ et $-\infty$.
\end{itemize}
\end{minipage}
\begin{minipage}[r]{0.6\linewidth}
\begin{tikzpicture}
   \tkzTabInit[color, colorC = blue!15, colorL = green!15]{$x$ / 1 ,$f$ / 3}{$-\infty$, $-1$,$3$, $+\infty$}

   \tkzTabVar{-/$-\infty$,+/$2$,-/$-1$,+/$+\infty$}
\end{tikzpicture}
\end{minipage}
\end{ex}
\begin{ex}
\begin{minipage}[l]{0.35\linewidth}
\begin{itemize}
  \item La droite d'equation $y=-2$ est asymptote à $(C_f)$ au voisinage de $+\infty$.
  \item La droite $(\Delta
  ): y=-x-2$ est une asymptote oblique à $(C_f)$ au voisinage de $-\infty$ ($(C_f)$ est au dessus de $\Delta$).
  \item La droite d’équation $x=0$ est une asymptote verticale à $(C_f)$.
  \item l'équation $f(x)=0$ admet une unique solution $a$ telle que $1<a<2$.
\end{itemize}
\end{minipage}
\begin{minipage}[r]{0.6\linewidth}
\begin{tikzpicture}
   \tkzTabInit[color, colorC = blue!15, colorL = green!15]{$x$ / 1 ,$f$ / 3}{$-\infty$, $-2$,$0$, $+\infty$}

   \tkzTabVar{+/$+\infty$,-/$1$,+D+/ $+\infty$ /$+\infty$ ,-/$-2$}
\end{tikzpicture}
\end{minipage}
\end{ex}
\begin{ex}
\begin{minipage}[l]{0.5\linewidth}
\begin{itemize}
  \item $(C_f)$ admet une asymptote horizontale d'equation $y=-3$ au voisinage de $+\infty$.
  \item $(C_f)$ admet une asymptote verticale en $1$ .
  \item $(C_f)$ coupe l'axe des abscisses en deux points $A(0;0)$ et $B(2,0)$ selon l'image).
  \item $(C_f)$ admet une branche parabolique de direction l'axe des abscisses au voisinage de $-\infty$
\end{itemize}
\end{minipage}
\begin{minipage}[r]{0.5\linewidth}
\begin{tikzpicture}
   \tkzTabInit[color, colorC = blue!15, colorL = green!15]{$x$ / 1 ,$f$ / 3}{$-\infty$, $1$, $+\infty$}

   \tkzTabVar{+/$+\infty$,-D+/ $-\infty$ /$+\infty$ ,-/$-3$}
\end{tikzpicture}
\end{minipage}
\end{ex}
\end{document}