\documentclass[a4paper,12pt]{article}
\usepackage[left=1.00cm, right=1.00cm, top=2cm, bottom=1.50cm]{geometry}
\usepackage[utf8]{inputenc}
\usepackage[french]{babel}
\usepackage{amsmath, amssymb}
\usepackage{graphicx}
\usepackage{xcolor}
\usepackage{multicol}
\usepackage{enumitem}
\usepackage{mathrsfs}
\usepackage{tcolorbox,varwidth}
\usepackage{fontspec}

\usepackage{colortbl}
\usepackage{libertinus}

\tcbuselibrary{skins,breakable}
\usepackage{tikz}
\usetikzlibrary{calc}
\usetikzlibrary{shadows}
\usepackage{tabularx, array}
\usepackage{fancyhdr}
\usepackage{setspace}


\usepackage{bidi}
\newfontfamily\arabicfont[Script=Arabic,Scale=1.1]{Amiri}

% define tight enemerate on first level only {1}
\newlist{tightenum}{enumerate}{1}
\setlist[tightenum]{label=\textbf{\arabic*)}, leftmargin=*, itemsep=0pt, topsep=0pt, parsep=0pt, partopsep=0pt}



% --- Basic Settings ---
\def\professor{R. MOSAID}
\def\classname{2BAC.PC/SVT}
\def\examtitle{Devoir 01 - S01}
\def\schoolname{\textbf{Lycée :} Taghzirt}
\def\academicyear{2025/2026}
\def\subject{Mathématiques}
\def\duration{2h}
\def\secondtitle{\small Par: Pr. MOHAMED JOUAHRI}
\def\province{Direction provinciale de\\ Beni Mellal}
\def\logo{\includegraphics[width=\linewidth]{images/logo-men.png}}
\def\wsite{\color{magenta}\texttt{www.mosaid.xyz}}
\def\ddate{\hfill \number\day/\number\month/\number\year~~}
\def\bottommsg{Bonne chance!}
\setstretch{1.5}
\everymath{\displaystyle}

% --- Exercise Theme 11 ---
% --- Theme 11: Chevron arrow banner (as in scanned sheet) ---
\definecolor{arrowblue}{RGB}{0,140,180}
\definecolor{bannerblue}{RGB}{210,240,240}

\newtcolorbox{exothemeeleven}[2][]{%
  enhanced,
  breakable,
  width=\linewidth,
  colback=white,
  colframe=white,
  boxrule=0pt,
  left=0pt, right=0pt, top=5pt, bottom=0pt,
  boxsep=0pt,
  before skip=5pt, after skip=5pt,
  interior style={fill=none, top color=white, bottom color=white},
  title={\#2},
  boxed title style={empty, boxrule=0pt, top=0pt, bottom=0pt},
  attach boxed title to top left={yshift=0pt},
  varwidth boxed title=0.9\linewidth,
  before upper={\parskip=4pt},
  overlay unbroken={
    % Chevron banner background
    \begin{scope}[shift={(frame.north west)}]
      \fill[bannerblue] (0,0) rectangle (\linewidth,0.8);
      \fill[arrowblue] (-0.4,0) -- (0.4,0.4) -- (-0.4,0.8) -- (0,0.4) -- cycle;
      \node[anchor=west, font=\bfseries] at (0.4,0.4)
        {\tcbtitletext};
    \end{scope}
  },
  #1
}


\newcommand{\printexo}[3]{%
  \if\relax\detokenize{\#2}\relax
    \def\fulltitle{Exercice #1}%
  \else
    \def\fulltitle{Exercice #1~#2}%
  \fi
  \begin{exothemeeleven}{\fulltitle}#3\end{exothemeeleven}%
  \vspace{0.2cm}%
}
% --- Header Style 9 ---
\newcommand{\printheadnine}{%

  \arrayrulecolor{lightgray}

  \begin{tabular}{m{0.3\textwidth} m{0.34\textwidth} m{0.3\textwidth}}
      \textbf{\classname} & \centering \textbf{\examtitle}
      & \ddate \\
      \wsite & \centering \large\textbf{\secondtitle}
      &\hfill
        \begin{tabular}{|c}
          \hline
          \textbf{~~\professor}
        \end{tabular}\\
      \hline
  \end{tabular}

  \arrayrulecolor{black} % restore default if needed
}

\fancyhf{}%
\renewcommand{\headrulewidth}{0pt}%
\renewcommand{\footrulewidth}{0pt}%
\setlength{\headheight}{47pt}%
\setlength{\headsep}{0pt}%
\fancyhead[C]{%
    \printheadnine
}%
\pagestyle{fancy}%
\begin{document}

% Exercise 1
\printexo{1}{}{
\begin{tightenum}[label=\arabic*.]
    \item Mettre en ordre croissant les nombres \(\sqrt[6]{5}\) ; \(\sqrt[4]{3}\) \hfill (1pt)
    \item Résoudre dans \(\mathbb{R}\) :
        ~$ \sqrt[3]{x^2 + 2} = \sqrt[3]{2x + 1} \quad ; \quad \sqrt[3]{4x - 5} \leq 3 $~ \hfill (1.5pt)
    \item Calculer les limites suivantes :
        ~$ \lim_{x \to 1} \sqrt[3]{x^3 + x + 6} $~ \quad ; \quad
        ~$ \lim_{x \to +\infty} \sqrt[3]{8x^3 + 5 }- 2x $~ \hfill (1.5pt)
    \item Calculer \(f'(x)\) dans les cas suivants :
        ~$ f(x) = \sin(3x + 2) $~
        ~$ I = \mathbb{R}_+^* $~ \quad ; \quad
        ~$ f(x) = \sqrt[6]{(x^2 + 5x)} \quad I = \mathbb{R}_+^* $~ \hfill (2pt)
\end{tightenum}
}

% Exercise 2
\printexo{2}{}{
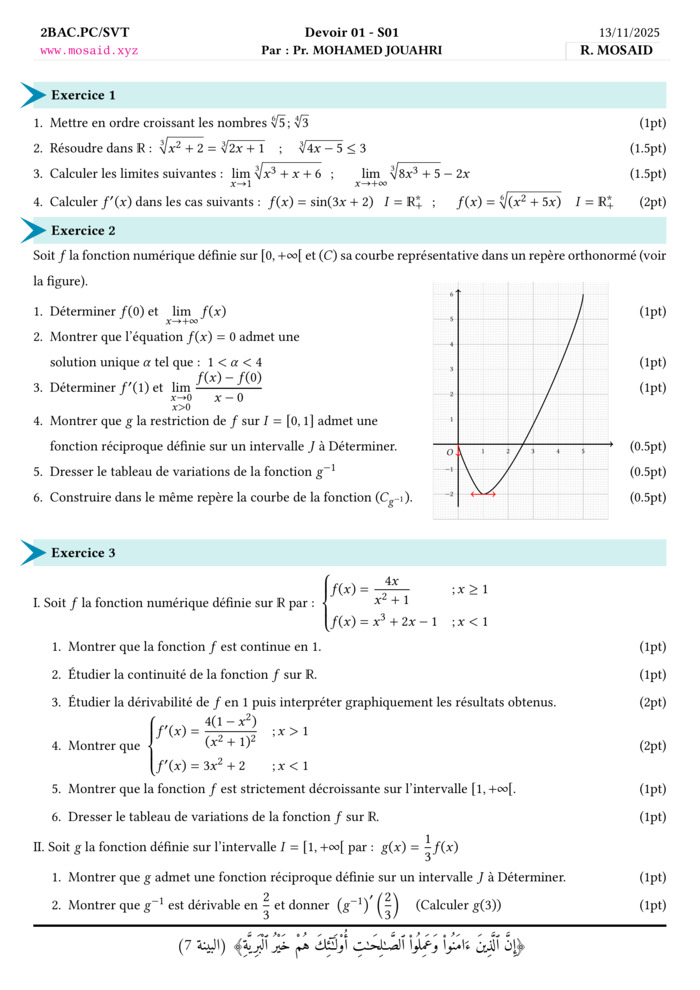
Soit \(f\) la fonction numérique définie sur \([0, +\infty[\) et \((C)\) sa courbe représentative dans un repère orthonormé (voir la figure).
\begin{tightenum}[label=\arabic*.]
    \item Déterminer \(f(0)\) et
        ~$ \lim_{x \to +\infty} f(x) $~ \hfill (1pt)
    \item Montrer que l’équation \(f(x) = 0\) admet une \\ solution unique \(\alpha\) tel que :
        ~$ 1 < \alpha < 4 $~ \hfill (1pt)
    \item Déterminer \(f'(1)\) et
        ~$ \lim_{\substack{x \to 0 \\ x > 0}} \frac{f(x) - f(0)}{x - 0} $~ \hfill (1pt)
    \item Montrer que \(g\) la restriction de \(f\) sur \(I = [0, 1]\) admet une \\fonction réciproque définie sur un intervalle \(J\) à Déterminer. \hfill (0.5pt)
    \item Dresser le tableau de variations de la fonction \(g^{-1}\) \hfill (0.5pt)
    \item Construire dans le même repère la courbe de la fonction \((C_{g^{-1}})\). \hfill (0.5pt)
\end{tightenum}
  \begin{tikzpicture}[scale=0.75, overlay, remember picture, xshift=17cm, yshift=3.5cm]
    % Grid (for visual reference, can be removed)
    \draw[step=0.1cm, gray!20, very thin] (-1,-3) grid (6,6.5);
    \draw[step=1cm, gray!50, thin] (-1,-3) grid (6,6.5);

    % Axes
    \draw[->, thick] (-1,0) -- (6.2,0)  ;
    \draw[->, thick] (0,-2.5) -- (0,6.2) ;
    \node[below left,font=\scriptsize] at (0,0) {$O$};

    \foreach \x in {1,2,...,5}{
      \node[below,font=\tiny] at (\x,0) {$\x$};
    }

    \foreach \x in {-2,-1,...,6}{
      \ifnum\x=0
        % do nothing for 0
      \else
        \node[left,font=\tiny] at (0,\x) {$\x$};
      \fi
    }

    \draw[looseness=0.3,  thick] (0,0) to[out=-90,in=-180] (1,-2) to[out=0,in=-90] (5,6);
    % Highlight x-axis part near vertex
    \draw[red, thick, <->] (0.5,-2) -- (1.5,-2);
    \draw[red, thick, ->] (0,0) -- (0,-0.5);

    % Optional control points (remove if not needed)
    %\foreach \x/\y in {0/0, 1/-2, 2.8/0, 3/0.5, 4/3, 5/6}{
    %    \filldraw[red] (\x,\y) circle (1pt);
    %}

\end{tikzpicture}
}

% Exercise 3
\printexo{3}{}{
I. Soit \(f\) la fonction numérique définie sur \(\mathbb{R}\) par :
    ~$
    \begin{cases}
    f(x) = \frac{4x}{x^2 + 1} & ; x \geq 1 \\
    f(x) = x^3 + 2x - 1 & ; x < 1
    \end{cases}
    $~
\begin{enumerate}[label=\arabic*.]
    \item Montrer que la fonction \(f\) est continue en 1. \hfill (1pt)
    \item Étudier la continuité de la fonction \(f\) sur \(\mathbb{R}\). \hfill (1pt)
    \item Étudier la dérivabilité de \(f\) en 1 puis interpréter graphiquement les résultats obtenus. \hfill (2pt)
      \item Montrer que
        ~$
        \begin{cases}
        f'(x) = \frac{4(1 - x^2)}{(x^2 + 1)^2} & ; x > 1 \\
        f'(x) = 3x^2 + 2 & ; x < 1
        \end{cases}
        $~ \hfill (2pt)
    \item Montrer que la fonction \(f\) est strictement décroissante sur l’intervalle \([1, +\infty[\). \hfill (1pt)
    \item Dresser le tableau de variations de la fonction \(f\) sur \(\mathbb{R}\). \hfill (1pt)
\end{enumerate}
II. Soit \(g\) la fonction définie sur l’intervalle \(I = [1, +\infty[\) par :
        ~$ g(x) = \frac{1}{3}f(x) $
\begin{enumerate}[label=\arabic*.]
    \item Montrer que \(g\) admet une fonction réciproque définie sur un intervalle \(J\) à Déterminer. \hfill (1pt)
    \item Montrer que \(g^{-1}\) est dérivable en \(\frac{2}{3}\) et donner
        ~$ \left(g^{-1}\right)'\left(\frac{2}{3}\right) \quad (\text{Calculer } g(3)) $~ \hfill (1pt)
\end{enumerate}
}
\vspace*{-0.5cm}
\begin{center}
   \vskip 2pt \hrule height 2pt \vskip 2pt \RL{\arabicfont ﴿إِنَّ ٱلَّذِينَ ءَامَنُوا۟ وَعَمِلُوا۟ ٱلصَّـٰلِحَـٰتِ أُو۟لَـٰٓئِكَ هُمْ خَيْرُ ٱلْبَرِيَّةِ﴾ (البينة 7) }
\end{center}


\end{document}