\documentclass[12pt,a4paper]{article}
\usepackage{tabularx}
\usepackage{booktabs}
\usepackage{ragged2e}
\usepackage[left=1.00cm, right=1.00cm, top=0.50cm, bottom=1.00cm]{geometry}
\usepackage{amsmath,amsfonts,amssymb}
\usepackage{mathrsfs}
\usepackage{enumitem}
\usepackage{multirow}
\usepackage{xcolor}
\usepackage[ddmmyyyy]{datetime}


\usepackage{polynom}
\usepackage{draftwatermark}
\usepackage{hyperref}

\polyset{style=D}% A,B,C,D

\hypersetup{
    colorlinks=true,
    linkcolor=blue
}
\definecolor{cc}{rgb}{236,0,140}
\newcommand{\mylink}{\href{https://mosaid.xyz/cc}{www.mosaid.xyz}}

\SetWatermarkText{\color{cc!10!white}{www.mosaid.xyz}}
\SetWatermarkLightness{0.95}
\SetWatermarkScale{0.8}

\newcolumntype{C}{>{\Centering\arraybackslash}X}
\newcolumntype{A}{>{\centering\arraybackslash}m{1em}}%

\begin{document}
\thispagestyle{empty}
\noindent
\begin{center}
    \begin{tabular}{@{}p{0.22\textwidth}p{0.57\textwidth}p{0.17\textwidth}}
        %\toprule
            \multirow{2}{*}{\parbox{\linewidth}{Prof MOSAID \newline \mylink }}
            & \Centering {Correction Série : Polynomes - Exercice 3} & \hfill  TCS \\
        \bottomrule
    \end{tabular}
\end{center}
\noindent
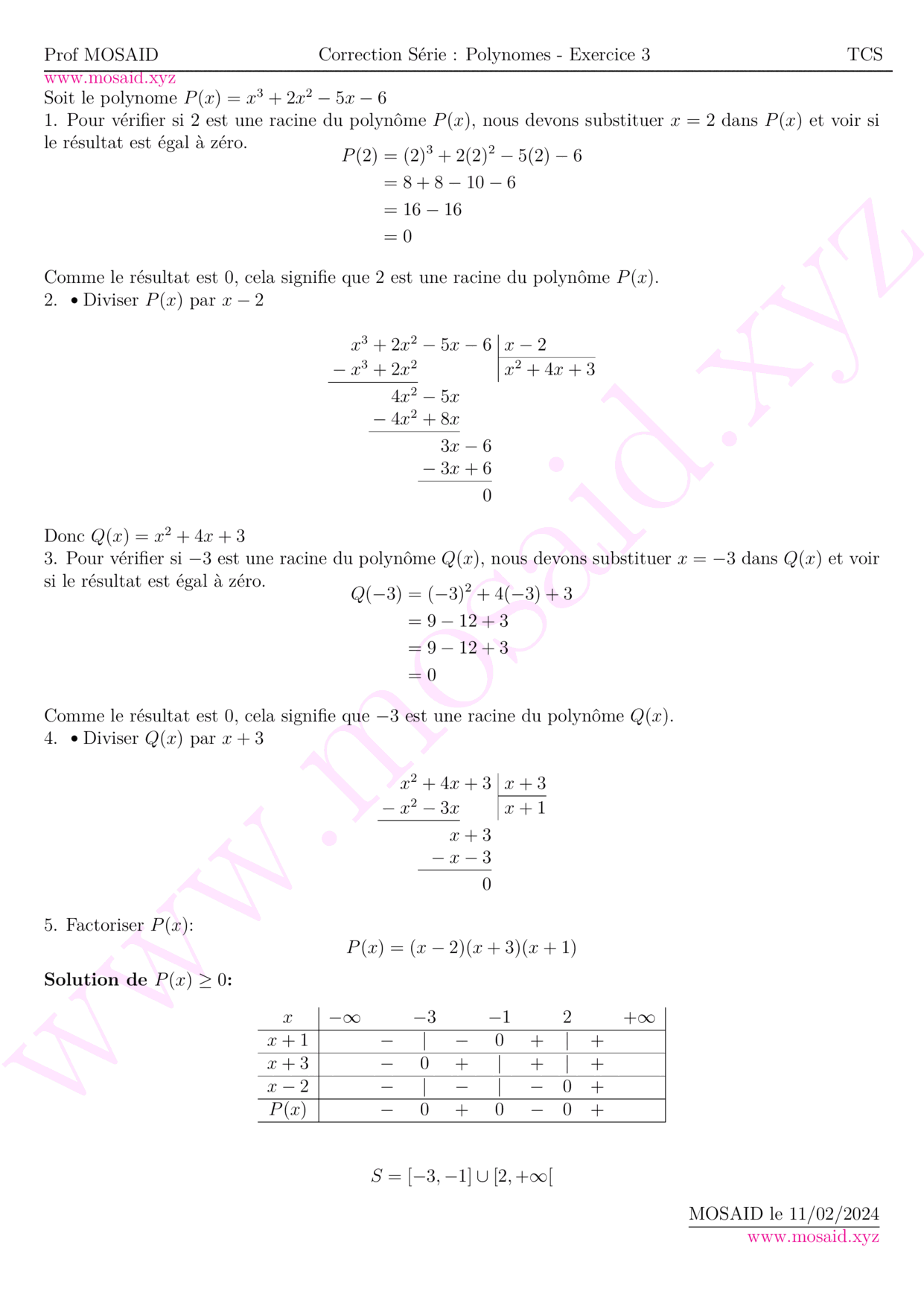
Soit le polynome \(P(x)=x^3+2x^2-5x-6\)\\
1. Pour vérifier si \(2\) est une racine du polynôme \(P(x)\), nous devons substituer \(x = 2\) dans \(P(x)\) et voir si le résultat est égal à zéro.
\vspace*{-1.5cm}
\begin{center}
\begin{align*}
P(2) &= (2)^3 + 2(2)^2 - 5(2) - 6 \\
&= 8 + 8 - 10 - 6 \\
&= 16 - 16 \\
&= 0
\end{align*}
\end{center}
Comme le résultat est \(0\), cela signifie que \(2\) est une racine du polynôme \(P(x)\).\\
2. {\large\textbullet}Diviser \(P(x)\) par \(x-2\)\\
\[ \polylongdiv{x^3+2x^2-5x-6}{x-2} \] \\
Donc \(Q(x)=x^2+4x+3\)\\
3. Pour vérifier si \(-3\) est une racine du polynôme \(Q(x)\), nous devons substituer \(x = -3\) dans \(Q(x)\) et voir si le résultat est égal à zéro.
\vspace*{-1.5cm}
\begin{center}
\begin{align*}
Q(-3) &= (-3)^2 + 4(-3) + 3 \\
&= 9 - 12 + 3 \\
&= 9 - 12 + 3 \\
&= 0
\end{align*}
\end{center}
Comme le résultat est \(0\), cela signifie que \(-3\) est une racine du polynôme \(Q(x)\).\\
4. {\large\textbullet}Diviser \(Q(x)\) par \(x+3\)\\
\[ \polylongdiv{x^2+4x+3}{x+3} \] \\
5. Factoriser \(P(x)\):
\[P(x)=(x-2)(x+3)(x+1)\]
\noindent
\textbf{Solution de \(P(x) \ge 0\):}
\begin{center}
\begin{tabular}{c|*{9}{>{\(}c<{\)}}|}
\(x\)   & -\infty &  & -3 & & -1 & & 2 & & +\infty \\
\hline
\(x+1\)&&-&|&-&0&+&|&+&\\
\hline
\(x+3\)&&-&0&+&|&+&|&+&\\
\hline
\(x-2\)&&-&|&-&|&-&0&+&\\
\hline
\(P(x)\)&&-&0&+&0&-&0&+&\\
\hline
\end{tabular}
\\
\vspace*{1cm}
\(S=[-3,-1]\cup[2,+\infty[\)
\end{center}
\textcolor{white}{.}\hfill \underline{MOSAID le \today}\\
\textcolor{white}{.}\hfill \mylink
\end{document}