---

---

---

    

\documentclass[12pt, a4paper]{exam}%answers,addpoints, answers,
\usepackage[left=2cm,right=0.5cm,top=0cm,bottom=1cm]{geometry}   % Set page margins
\usepackage[french]{babel}
\usepackage{fontspec}
\usepackage{calligra} % For calligraphy font
\usepackage[T1]{fontenc}
\usepackage{amsmath, amssymb,mathrsfs}
\usepackage{tikz, pgfplots}
\pgfplotsset{compat=1.18}
\usetikzlibrary{shapes,decorations.text}
\usetikzlibrary{decorations.pathmorphing,shadows}
\usepackage{xcolor}
\usepackage{setspace}
\usepackage[ddmmyyyy]{datetime}
\usepackage{xparse} % Required for advanced argument parsing

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%% Start config %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

\def\classname{TCSF}
\def\dsname{Contrôl n$^\circ$2/2h}
\def\dsletter{C}
\def\prof{MOSAID}

% borders right margin
\def\bordersrmargin{0.5}
% borders height in answers mode
\def\bordersheighta{28}
% borders height
\def\bordersheight{14}

\newif\ifprintdouble
% Uncomment the next line to print the ds twice on the same page
\printdoubletrue

%%%%%%%%%%%%%%%%%%%%%%%%%%%% End config %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

\pointname{}
\pointformat{\textbf{\textit{(\thepoints)}}}

% Exam settings
\pointsinmargin
%\colorfillwithlines
%\definecolor{FillWithLinesColor}{gray}{0.8}
\colorfillwithdottedlines
\definecolor{FillWithDottedLinesColor}{gray}{0.7}
\unframedsolutions
\renewcommand{\solutiontitle}{\noindent\textbf{}\enspace}
\SolutionEmphasis{\itshape\small}
\SolutionEmphasis{\color{red}\bfseries}

\newcommand{\tb}{\tikz[baseline=-0.6ex]{\fill (0,0) circle (2pt);}~}

\newcommand{\ccc}[1]{
    \begin{tikzpicture}[overlay, remember picture]
        \node[circle, inner sep=3pt, draw=black, outer sep=0pt] at (0.5,0.2) {\#1};
    \end{tikzpicture}
}

\newcommand{\luck}[1]{
    \begin{tikzpicture}[overlay, remember picture]
        \node[] at (#1) {\scalebox{2}{\textbf{\textcolor{blue}{\calligra Good Luck!}}}};
      %rotate=25
    \end{tikzpicture}
}

\NewDocumentCommand{\sticker}{O{6.5} O{-10} m m}{%
  \begin{tikzpicture}[overlay, remember picture, shift={(#3)}]
    % Rectangle with wavy border and text node
    \node[
        shape=rectangle, % Rectangle shape
        decorate,
        decoration={random steps, segment length=2mm, amplitude=1.5mm}, % Wavy effect
        fill=cyan!20, % Background color
        draw=red, % Border color
        line width=1pt, % Border thickness
        inner sep=5pt, % Padding between text and border
        text width=#1, % Width of the text box
        align=center, % Center the text
        rotate=#2, % Rotation angle
    ] (sticker) at (0, 0) { % Position of the sticker
        #4
    };

    % Label
    \node[] at ([xshift=0.5cm]sticker.north west) {
       \includegraphics[width=0.9cm]{pin.png}
    };
  \end{tikzpicture}%
}



\newcommand{\dangericon}{%
    \tikz[baseline=-0.5ex]{
        \draw[draw=red, line width=1mm] (0,0.5) -- (0.7,-0.6) -- (-0.7,-0.6) -- cycle;
        \node[inner sep=0pt, font=\bfseries, scale=2] at (-0.05,-0.2) {!};
    }%
}

\newcommand{\stamp}[2]{
\begin{tikzpicture}[remember picture, overlay]
\coordinate (A) at (#1,#2);
\draw[red!50] (A) circle (1.9cm);
% Draw the inner circle
\draw[red!50] (A) circle (1.4cm);
% Draw the curved line
\draw[red!50, decorate, decoration={text along path,
    text={|\fontspec{DejaVu Sans}\color{red!75}\bfseries|★MOSAID RADOUAN★},
    text align={align=center}, raise=-3pt}] (A) ++ (180:1.6cm) arc (180:0:1.6cm);
\draw[decorate, decoration={text along path,
    text={|\fontspec{DejaVu Sans}\color{red!75}\bfseries|∞★~mosaid.xyz~★∞ },
    text align={align=center}, raise=-6.5pt}] (A) ++ (180:1.53cm) arc (-180:0:1.53cm);
\node[red!75,font=\fontsize{48}{48}\fontspec{DejaVu Sans}\bfseries\selectfont] at (A) {✷};
\end{tikzpicture}
}

\newcommand{\borders}{%
  \tikz[remember picture, overlay, xshift=-0.5cm]{
    \ifprintanswers
        \def\bheight{\bordersheighta}
    \else
        \def\bheight{\bordersheight}
    \fi
    \draw[gray, thick] (\bordersrmargin,-1.2) -- (\bordersrmargin,-\bheight);
    \draw[gray, thick] (\bordersrmargin,-1.2) -- (\textwidth,-1.2);
    \node[black] at (0.5,-0.25) {\textbf{\classname}};
    \node[magenta] at (1.6,-0.6) {\textbf{www.mosaid.xyz}};
    \node[black,xshift=-2cm] at (\textwidth,-0.25) {\textbf{\today}};
    \node[black,xshift=-2cm] (A) at (\textwidth,-0.9)  {\textbf{Prof : \prof}};
    \node[black,xshift=-0.5cm] at (0.5\textwidth,-0.5) {
        \ifprintanswers
            \textbf{Correction \dsname }
        \else
            \textbf{\dsname}
        \fi
        \ccc{\dsletter}
    };
    \draw[gray, thick] (A.south west) -- ++(0,0.7) -- ++(3.8,0) ;
    \node[magenta] at (0.9\textwidth,-1.4) {\textbf{www.mosaid.xyz}};
  }%
}

\newcommand{\exo}[1]{%
    \begin{tikzpicture}
        % Node for the text
        \node[] (text) at (0,0) {\textbf{\#1}};
        % Shadow (calculated based on the text width)
        \fill[black] ([xshift=0.1cm, yshift=-0.1cm]text.south west)
                     rectangle ([xshift=0.1cm, yshift=-0.1cm]text.north east);
        % Main box (calculated based on the text width)
        \draw[fill=white] (text.south west) rectangle (text.north east);
        % Text inside the box
        \node[] at (text) {\textbf{\#1}};
    \end{tikzpicture}%
}

%\footer{}{Page \thepage\ of \numpages}{}

\everymath{\displaystyle}
%\setstretch{1.2}
\newenvironment{mycontent}{%
\noindent
\borders\\[1.5cm]
%%%%%%%%%%%%%%%%%%%%%%%%%%%% Start of the exam %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
\noindent
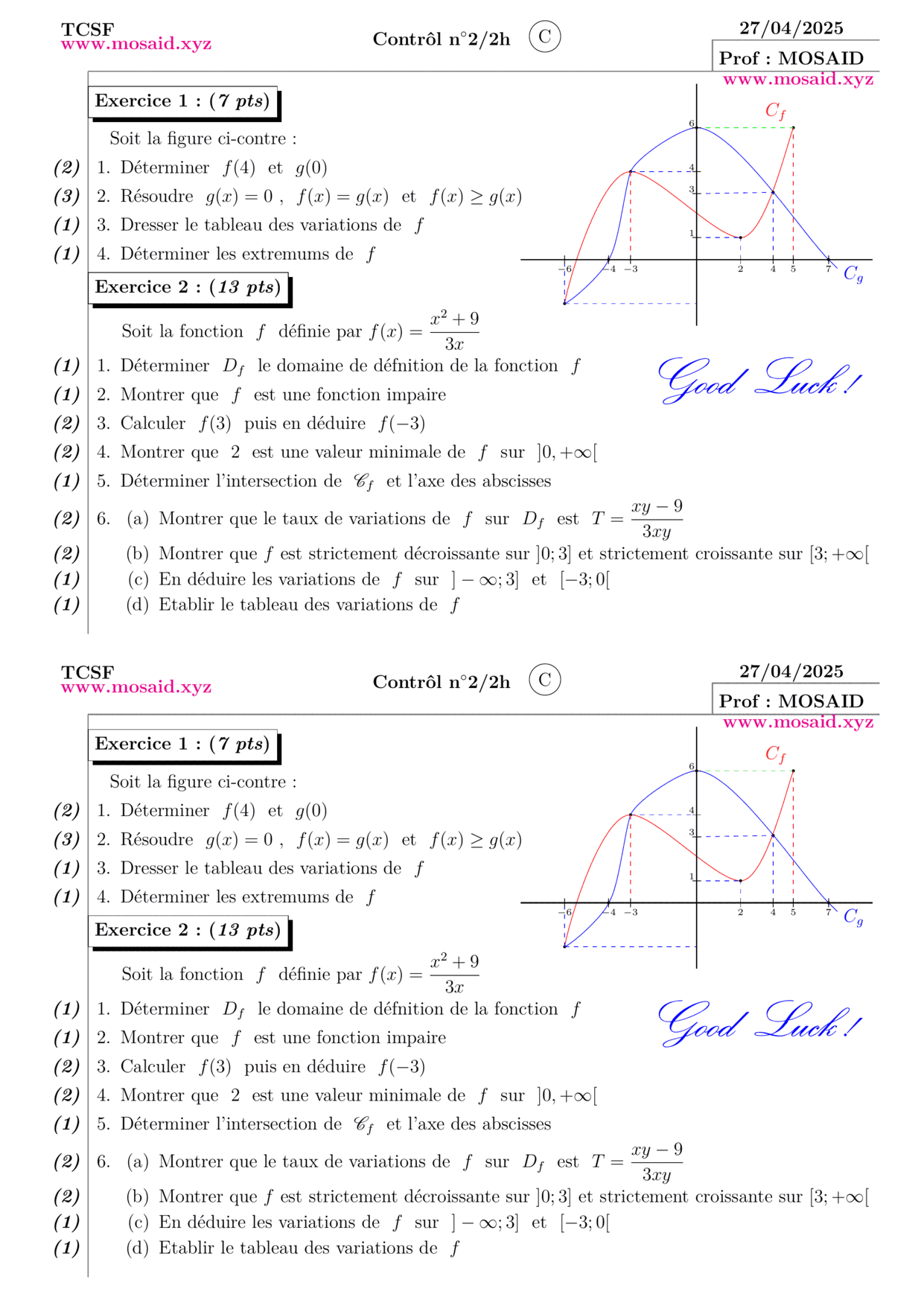
\exo{Exercice 1: (\textit{7 pts}) }\\
\hspace*{0.5cm}Soit la figure ci-contre:
\begin{questions}
  \question[2]
  Déterminer ~$f(4)$~ et ~$g(0)$~
  \question[3]
  Résoudre  ~$g(x)=0$~, ~$f(x)=g(x)$~ et ~$f(x)\ge g(x)$~
  \question[1]
  Dresser le tableau des variations de ~$f$~
  \question[1]
  Déterminer les extremums de ~$f$~
\begin{tikzpicture}[overlay, remember picture,xshift=7cm]
    \coordinate (A) at (-3,-1);
    \coordinate (B) at (-1.5,2);
    \coordinate (C) at (-2,0);
    \coordinate (D) at (0,3);
    \coordinate (E) at (3,0);
    \coordinate (F) at (2.2,3);
    \coordinate (G) at (1,0.5);
    \coordinate (H) at (1.74,1.53);
    \coordinate (K) at (1.92,2);
    \draw[blue, looseness=0.5] (A) to[out=25,in=-110] (C)
                                   to[out=55,in=-110] (B)
                                   to[out=68,in=180] (D)
                                   to[out=0, in=135] (E) -- (3.2,-0.2)
                                   node[above right, yshift=-0.5cm] {$C_g$};

    \draw[red, looseness=0.5] (A) to[out=80,in=180] (B)
                                  to[out=0,in=180] (G)
                                  to[out=0,in=-110] (F)
                                  node[above left] {$C_f$};

    \foreach \point in {A,B,C,D,E,F,G,H} {
      \edef\temp{\noexpand\fill (\point) circle (1pt);}
      \temp
    }
    \draw[blue, dashed] (A) -- (0,-1);
    \draw[green, dashed] (D) -- (F);
    \draw[blue, dashed] (0,0.5) -- (G);

    \draw[blue, dashed] (A) -- (-3,0);
    \draw[blue, dashed] (B) -- (0,2);
    \draw[blue, dashed] (1,0) -- (G);
    \draw[blue, dashed] (1.74,0) -- (H)--(0,1.5);
    \draw[red, dashed] (B) -- (-1.5,0);
    \draw[red, dashed] (2.2,0) -- (F);
    \draw[thick] (0,-1.5) -- (0,4);
    \draw[thick] (-4,0) -- (4,0);
    \foreach \x/\l in {-3/-6,-2/-4,-1.5/-3,1/2,1.74/4,2.2/5,3/7} {
    \draw (\x,-0.1) -- (\x,0.1) node [below, yshift=-0.1cm,font=\fontsize{6}{8}\selectfont] {$\l$} ;
    }
    \foreach \x/\l in {0.5/1,1.5/3,2/4,3/6} {
    \draw (-0.1,\x) -- (0.1,\x) node [left, yshift=0.1cm,font=\fontsize{6}{8}\selectfont] {$\l$} ;
    }
\end{tikzpicture}
\end{questions}
\exo{Exercice 2: (\textit{13 pts}) }\\
%\stamp{15.5}{4}
\luck{15,-1}
\hspace*{0.5cm}Soit la fonction ~$f$~ définie par $f(x) = \frac{x^2+9}{3x}$
\begin{questions}
  \question[1]
  Déterminer ~$D_f$~ le domaine de défnition de la fonction ~$f$~
  \question[1]
  Montrer que ~$f$~ est une fonction impaire
  \question[2]
  Calculer ~$f(3)$~ puis en déduire ~$f(-3)$~
  \question[2]
  Montrer que ~$2$~ est une valeur minimale de ~$f$~ sur ~$]0,+\infty[$~
  \question[1]
  Déterminer l'intersection de ~$\mathscr{C}_f$~ et l'axe des abscisses
  \question
  \begin{parts}
      \part[2]
        Montrer que le taux de variations de ~$f$~ sur ~$D_f$~ est ~$T= \frac{xy-9}{3xy}$~
      \part[2]
      Montrer que $f$ est strictement décroissante sur $]0;3]$ et strictement croissante sur $[3;+\infty[$
      \part[1]
      En déduire les variations de ~$f$~ sur ~$]-\infty;3]$~ et ~$[-3;0[$~
      \part[1]
      Etablir le tableau des variations de ~$f$~
  \end{parts}
\end{questions}
%%%%%%%%%%%%%%%%%%%%%%%%%%%% End exam %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
}% end newenvironment

\begin{document}
  \ifprintanswers
    \begin{mycontent}\end{mycontent}
  \else
      %
  \fi
 % \newpage
  \noprintanswers
  \begin{mycontent}\end{mycontent}
  \ifprintdouble
    \textcolor{white}{.}\\
    \begin{mycontent}\end{mycontent}
  \fi
\end{document}