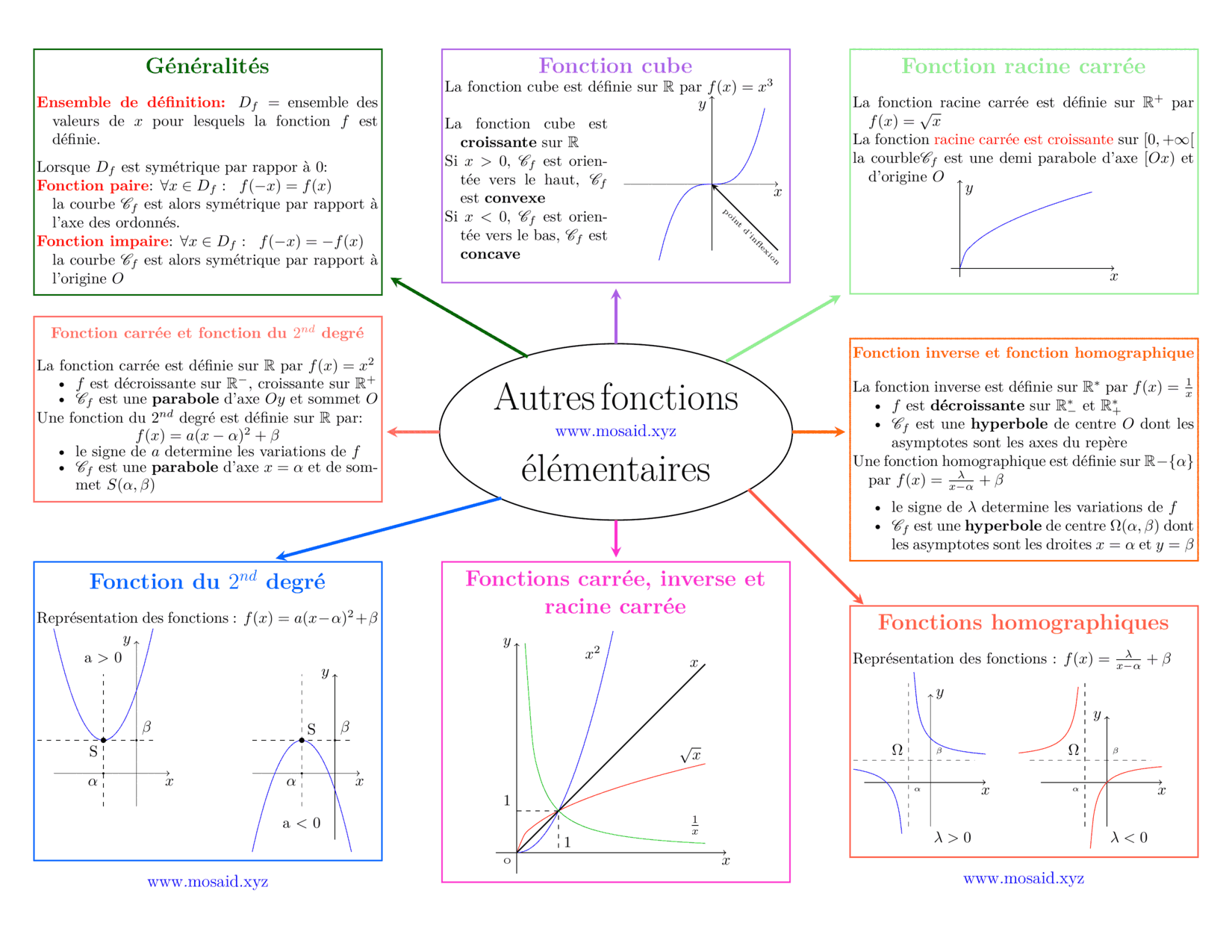
\documentclass[landscape]{article}
\usepackage[margin=0.75cm]{geometry}
\usepackage{amsmath}
\usepackage{amssymb}
\usepackage{mathrsfs}
\usepackage{enumitem}
\usepackage{xcolor}
\usepackage{mdframed}
\usepackage{multicol}
\usepackage{tikz}
\usetikzlibrary{calc}
\usepackage{tikzpagenodes}
\usepackage[hidelinks]{hyperref}

% Define colors for each section
\definecolor{part1color}{RGB}{0,100,0}
\definecolor{part2color}{RGB}{255,105,100}
\definecolor{part3color}{RGB}{0,100,255}
\definecolor{part4color}{RGB}{173,100,230}
\definecolor{part5color}{RGB}{144,238,144}
\definecolor{part6color}{RGB}{255,100,0}
\definecolor{part7color}{RGB}{255,50,205}
\definecolor{part8color}{RGB}{255,99,71}

\newcommand{\mylink}{\href{https://mosaid.xyz}{www.mosaid.xyz}}

% Common settings for mdframed
\mdfdefinestyle{myframe}{
    linewidth=1pt,
    skipabove=-\baselineskip,
    skipbelow=-\baselineskip,
    leftmargin=0pt,
    rightmargin=0pt,
    innerleftmargin=1.5pt,
    innerrightmargin=2pt
}


% Define TikZ style for arrows
\tikzstyle{arrow} = [->,>=stealth,thick,black]

\newcommand{\hangingindent}[1]{\par\hangindent=1em\hangafter=1\noindent#1\par}

\begin{document}
% First Row
\noindent
\begin{minipage}[t][0.3\textheight][t]{0.3\textwidth}
    % Top-left content
    \begin{mdframed}[linecolor=part1color,style=myframe, linewidth=1pt]
    \begin{center}
            \section*{\textcolor{part1color}{Généralités}}
    \end{center}
    \hangingindent{\textcolor{red}{\textbf{Ensemble de définition:}} \(D_f=\) ensemble des valeurs
    de \(x\) pour lesquels la fonction \(f\) est définie.}
    \vspace*{0.2cm}
    \hangingindent{Lorsque \(D_f\) est symétrique par rappor à 0:}
    \hangingindent{\textcolor{red}{\textbf{Fonction paire}}: \(\forall x \in D_f: \hspace*{0.2cm}f(-x)=f(x)\) \\
    la courbe \(\mathscr{C}_f\) est alors symétrique par rapport à l'axe des ordonnés.}
    \hangingindent{\textcolor{red}{\textbf{Fonction impaire}}: \(\forall x \in D_f: \hspace*{0.2cm}f(-x)=-f(x)\) \\
    la courbe \(\mathscr{C}_f\) est alors symétrique par rapport à l'origine \(O\)}
    \end{mdframed}
\end{minipage}
\hfill
\begin{minipage}[t][0.3\textheight][t]{0.3\textwidth}
    % Top-center content
    \begin{mdframed}[style=myframe, linecolor=part4color, linewidth=1pt]
    \begin{center}
        \section*{\textcolor{part4color}{Fonction cube}}
    \end{center}
    \vspace*{-0.35cm}
    \hangingindent{La fonction cube est définie sur \(\mathbb{R}\) par \(f(x)= x^3\)}
    \vspace*{-0.75cm}
    \begin{multicols}{2}
        \vspace*{0.5cm}
        \hangingindent{La fonction cube est \textbf{croissante} sur \(\mathbb{R}\) }
        \hangingindent{Si \(x>0\), \(\mathscr{C}_f\) est orientée vers le haut, \(\mathscr{C}_f\) est \textbf{convexe}}
        \hangingindent{Si \(x<0\), \(\mathscr{C}_f\) est orientée vers le bas, \(\mathscr{C}_f\) est \textbf{concave}}
        \hangindent=1em
            \begin{tikzpicture}
            \draw[->] (-2,0) -- (1.5,0) node[below] {$x$};
            \draw[->] (0,-1.5) -- (0,2) node[below left] {$y$};
        \draw[domain=-1.2:1.2,smooth,variable=\x,blue] plot ({\x},{\x^3});
        \draw[arrow] (1.5,-1.5) -- (0,0) node[pos=0.3, below, sloped] {\tiny{point d'inflexion}};
            \end{tikzpicture}
    \end{multicols}
    \end{mdframed}

\end{minipage}
\hfill
\begin{minipage}[t][0.3\textheight][t]{0.3\textwidth}
    % Top-right content
    \begin{mdframed}[style=myframe, linecolor=part5color, linewidth=1pt]
    \begin{center}
        \section*{\textcolor{part5color}{Fonction racine carrée}}
    \end{center}
    \hangingindent{La fonction racine carrée est définie sur \(\mathbb{R}^{+}\) par \(f(x)= \sqrt{x}\)}
    \hangingindent{La fonction \textcolor{red}{racine carrée est croissante} sur \([0,+\infty[\) }
    \hangingindent{la courble\(\mathscr{C}_f\) est une demi parabole d'axe \([Ox)\) et d'origine \(O\)}
    \vspace*{-0.5cm}
    \begin{center}
        \hspace*{0.5cm}
        \begin{tikzpicture}
            \draw[->] (-0.2,0) -- (3.5,0) node[below] {$x$};
            \draw[->] (0,-0.2) -- (0,2) node[below right] {$y$};
            \draw[domain=0:3,smooth,variable=\x,blue] plot ({\x},{sqrt(\x)});
        \end{tikzpicture}
    \end{center}
    \end{mdframed}
\end{minipage}

\noindent
% Second Row
\begin{minipage}[t][0.3\textheight][t]{0.3\textwidth}
    % Middle-left content
    \begin{mdframed}[style=myframe, linecolor=part2color, linewidth=1pt]
    \setlength{\baselineskip}{2pt}
    \begin{center}
        \section*{\textcolor{part2color}{\fontsize{10}{8}\selectfont Fonction carrée et fonction du \(2^{nd}\) degré}}
    \end{center}
    \hangingindent{La fonction carrée est définie sur \(\mathbb{R}\) par \(f(x)= x^2\)}
    \begin{itemize}[topsep=0pt, partopsep=0pt, parsep=0pt, itemsep=0pt]
        \item \(f\) est décroissante sur \(\mathbb{R}^{-}\), croissante sur \(\mathbb{R}^{+}\)
        \item \(\mathscr{C}_f\) est une \textbf{parabole} d'axe \(Oy\) et sommet \(O\)
    \end{itemize}
    \hangingindent{Une fonction du \(2^{nd}\) degré est définie sur \(\mathbb{R}\) par:}
    \hangingindent{\centering  \(f(x)= a(x-\alpha)^2+\beta\)}
    \begin{itemize}[topsep=0pt, partopsep=0pt, parsep=0pt, itemsep=0pt]
        \item le signe de \(a\) determine les variations de \(f\)
        \item \(\mathscr{C}_f\) est une \textbf{parabole} d'axe \(x=\alpha\) et de sommet \(S(\alpha,\beta)\)
    \end{itemize}
    \end{mdframed}
\end{minipage}
\hfill
\begin{minipage}[t][0.3\textheight][t]{0.3\textwidth}
    % the ellipsis goes here
\end{minipage}
\hfill
\begin{minipage}[t][0.3\textheight][t]{0.3\textwidth}
    % Middle-right content
    \vspace*{0.5cm}
    \begin{mdframed}[style=myframe, linecolor=part6color, linewidth=1pt]
    \begin{center}
        \section*{\textcolor{part6color}{\fontsize{10}{8}\selectfont Fonction inverse et fonction homographique}}
    \end{center}
    \hangingindent{La fonction inverse est définie sur \(\mathbb{R}^{*}\) par \(f(x)= \frac{1}{x}\)}
    \begin{itemize}[topsep=0pt, partopsep=0pt, parsep=0pt, itemsep=0pt]
        \item \(f\) est \textbf{décroissante}  sur \(\mathbb{R}^{*}_{-}\) et \(\mathbb{R}^{*}_{+}\)
        \item \(\mathscr{C}_f\) est une \textbf{hyperbole} de centre \(O\) dont les asymptotes sont les axes du repère
    \end{itemize}
    \hangingindent{Une fonction homographique est définie sur \(\mathbb{R}-\{\alpha\} \)
        par \(f(x)= \frac{\lambda}{x-\alpha}+\beta\)}
    \vspace*{0.2cm}
    \begin{itemize}[topsep=0pt, partopsep=0pt, parsep=0pt, itemsep=0pt]
        \item le signe de \(\lambda\) determine les variations de \(f\)
        \item \(\mathscr{C}_f\) est une \textbf{hyperbole} de centre \(\Omega(\alpha,\beta)\)
        dont les asymptotes sont les droites \(x=\alpha\) et \(y=\beta\)
    \end{itemize}
    \end{mdframed}
\end{minipage}

\vspace*{-1cm}
\noindent
% Third Row
\begin{minipage}[t][0.3\textheight][t]{0.3\textwidth}
    % Bottom-left content
    \vspace*{0.5cm}
    \begin{mdframed}[style=myframe, linecolor=part3color, linewidth=1pt]
    \begin{center}
        \section*{\textcolor{part3color}{Fonction du \(2^{nd}\) degré}}
    \end{center}
    \hangingindent{Représentation des fonctions : \(f(x)= a(x-\alpha)^2+\beta\)}
    \begin{tikzpicture}[scale=0.75]
        % Parabole vers le haut (a > 0)
        \draw[->] (-2.5,0) -- (1,0) node[below] {$x$};
        \draw[->] (0,-1) -- (0,4) node[left] {$y$};
        \draw[domain=-2.5:0.5,smooth,variable=\x,blue] plot ({\x},{1.5*(\x+1)^2+1 });
        \filldraw (-1,1) circle (2pt) node[below left] {S};
        \draw[dashed] (-1,-1) -- (-1,3);
        \draw[dashed] (-3,1) -- (0.5,1);
        \fill (-1,0) circle (1pt) node[below left] {$\alpha$};
        \fill (0,1) circle (1pt) node[above right] {$\beta$};
        \node at (-1,3.5) {a > 0};
        % Parabole vers le bas (a < 0)
        \begin{scope}[xshift=6cm]
            \draw[->] (-2.5,0) -- (0.75,0) node[below] {$x$};
            \draw[->] (0,-2) -- (0,3) node[left] {$y$};
            \draw[domain=-2.5:0.5,smooth,variable=\x,blue] plot ({\x},{-1.5*(\x+1)^2+1 });
            \filldraw (-1,1) circle (2pt) node[above right] {S};
            \draw[dashed] (-1,-1) -- (-1,3);
            \draw[dashed] (-2.5,1) -- (0.5,1);
            \fill (-1,0) circle (1pt) node[below left] {$\alpha$};
            \fill (0,1) circle (1pt) node[above right] {$\beta$};
            \node at (-1,-1.5) {a < 0};
        \end{scope}
    \end{tikzpicture}
    \end{mdframed}
    \centering \fontsize{11}{10}\selectfont{\textcolor{blue}{\mylink}}
\end{minipage}
\hfill
\begin{minipage}[t][0.3\textheight][t]{0.3\textwidth}
    % Bottom-center content
    \vspace*{0.5cm}
    \begin{mdframed}[style=myframe, linecolor=part7color, linewidth=1pt]
    \begin{center}
        \section*{\textcolor{part7color}{Fonctions carrée, inverse et racine carrée}}
        \begin{tikzpicture}[scale=0.95]
            \draw[->] (-0.5,0) -- (5,0) node[below] {$x$};
            \draw[->] (0,-0.5) -- (0,5) node[left] {$y$};
            \draw[domain=0:2.3,smooth,variable=\x,blue] plot ({\x},{\x^2});
            \draw[domain=0:4.5,smooth,variable=\x,red] plot ({\x},{sqrt(\x)});
            \draw[domain=0.2:4.5,smooth,variable=\x,green] plot ({\x},{1/\x});
            \draw[domain=0:4.5,smooth,variable=\x,black,thick] plot ({\x},{\x});
            \draw[dashed] (0,1) -- (1,1) -- (1,0) ;
            \node[above right] at (1,0) {1};
            \node[above left] at (0,1) {1};
            \node[below left] at (0,0) {\tiny{O}};
            \node[above right] at (4,0.3) {\(\frac{1}{x}\)};
            \node[above right] at (1.5,4.5) {\(x^2\)};
            \node[above right] at (4,4.3) {\(x\)};
            \node[above right] at (3.75,2) {\(\sqrt{x}\)};
        \end{tikzpicture}
    \end{center}
    \end{mdframed}
\end{minipage}
\hfill
\begin{minipage}[t][0.3\textheight][t]{0.3\textwidth}
    % Bottom-right content
    \vspace*{1.5cm}
    \begin{mdframed}[style=myframe, linecolor=part8color, linewidth=1pt]
    \begin{center}
        \section*{\textcolor{part8color}{Fonctions homographiques}}
    \end{center}
    \hangingindent{Représentation des fonctions : \(f(x)= \frac{\lambda}{x-\alpha}+\beta\)}
    \begin{tikzpicture}[scale=0.5]
        \draw[->] (-3,0) -- (2.5,0) node[below] {$x$};
        \draw[->] (0,-2) -- (0,4) node[right] {$y$};
        \draw[domain=-0.75:2.5,smooth,variable=\x,blue] plot ({\x},{1/(\x+1)+1});
        \draw[domain=-3.5:-1.3,smooth,variable=\x,blue] plot ({\x},{1/(\x+1)+1});
        \draw[dashed] (-1,-2) -- (-1,4.5) ;
        \draw[dashed] (-3.5,1) -- (2,1) ;
        \node[above left] at (-1,1) {\(\Omega\)};
        \node[above right] at (0,1) {\fontsize{5}{4}\selectfont{\textbf{\(\beta\)}}};
        \node[below right] at (-1,0) {\fontsize{5}{4}\selectfont{\textbf{\(\alpha\)}}};
        \node at (1,-2.5) {\(\lambda>0\)};
            \begin{scope}[xshift=8cm]
            \draw[->] (-3,0) -- (2.5,0) node[below] {$x$};
            \draw[->] (0,-2) -- (0,3) node[left] {$y$};
            \draw[domain=-0.75:2.5,smooth,variable=\x,red] plot ({\x},{-1/(\x+1)+1});
            \draw[domain=-4:-1.3,smooth,variable=\x,red] plot ({\x},{-1/(\x+1)+1});
            \draw[dashed] (-1,-2) -- (-1,4.5) ;
            \draw[dashed] (-3.5,1) -- (2,1) ;
            \node[above left] at (-1,1) {\(\Omega\)};
            \node[above right] at (0,1) {\fontsize{5}{4}\selectfont{\textbf{\(\beta\)}}};
            \node[below left] at (-1,0) {\fontsize{5}{4}\selectfont{\textbf{\(\alpha\)}}};
            \node at (1,-2.5) {\(\lambda<0\)};
            \end{scope}
    \end{tikzpicture}
    \end{mdframed}
    \centering \fontsize{11}{10}\selectfont{\textcolor{blue}{\mylink}}
\end{minipage}


% Middle-center content
\begin{tikzpicture}[overlay, remember picture]
    % Calculate the middle point of the Core Information section
    \coordinate (hub) at ($(current page text area.south west)!0.5!(current page text area.north east)$);
    \draw[arrow] (hub) ++(0,1cm) ellipse (4cm and 2cm) node[align=center, text width=7cm]
    {\vspace*{0.5cm}\Huge{Autres fonctions} \\
    \vspace*{-0.25cm} \fontsize{11}{10}\selectfont{\textcolor{blue}{\mylink}} \\
    \vspace*{0.3cm} \Huge{élémentaires}};
    % Arrows pointing to other sections
    \draw[arrow, thick, line width=2pt, part4color] (hub) ++(0,3cm) -- ++(90:1.25cm) node[midway, above, sloped] {};
    \draw[arrow, thick, line width=2pt, part5color] (hub) ++(2.5cm,2.6cm) -- ++(30:3cm) node[midway, above, sloped] {};
    \draw[arrow, thick, line width=2pt, part6color] (hub) ++(4cm,1cm) -- ++(0:1.2cm) node[midway, above, sloped] {};
    \draw[arrow, thick, line width=2pt, part8color] (hub) ++(3cm,-0.3cm) -- ++(-45:3.7cm) node[midway, above, sloped] {};
    \draw[arrow, thick, line width=2pt, part7color] (hub) ++(0,-1cm) -- ++(-90:0.85cm) node[midway, above, sloped] {};
    \draw[arrow, thick, line width=2pt, part2color] (hub) ++(-4cm,1cm) -- ++(180:1.2cm) node[midway, above, sloped] {};
    \draw[arrow, thick, line width=2pt, part3color] (hub) ++(-2.6cm,-0.5cm) -- ++(195:5.3cm) node[midway, above, sloped] {};
    \draw[arrow, thick, line width=2pt, part1color] (hub) ++(-2cm,2.7cm) -- ++(150:3.6cm) node[midway, above, sloped] {};
\end{tikzpicture}

\end{document}