\documentclass{standalone}
\standaloneconfig{margin=2mm}
\usepackage{pgfplots}
\pgfplotsset{compat=newest}
\usetikzlibrary{calc}

\begin{document}

\begin{tikzpicture}[scale=1.00]
    \begin{axis}[axis lines=center,
        xlabel={$x$},
        ylabel={$y$},
    ytick={-1,0.5,1,1.5,2,3},
    xtick={-1.5,1,2.2,3},
    extra x ticks={-3,-2,0,1.75},
    extra x tick style={
        xticklabel style={xshift=-5pt, yshift=12pt},
        tick label style={font=\tiny},
        xticklabel pos=upper
    },
        %xtick=\empty,ytick=\empty,
    xmin=-4.5,xmax=5,
        ymin=-2,ymax=4,
        unbounded coords=jump,
    samples=200,
    xticklabel style={font=\tiny},
    yticklabel style={font=\tiny},
    ]
    \coordinate (A) at (0.05,-1.99);
    \coordinate (B) at (2,2);
    \coordinate (C) at (5,0.2);

    \draw[blue, looseness=0.5] (A) to[out=90,in=180] (B) to[out=0,in=180]  (C) node[above right] {$C_g$};

      \draw[<->,red] (1.5,2) - - (2.5,2);
      \draw[dashed,red] (2,2) - - (2,0);
      \draw[dashed,red] (2,2) - - (0,2);
     \end{axis}
\end{tikzpicture}
\end{document}

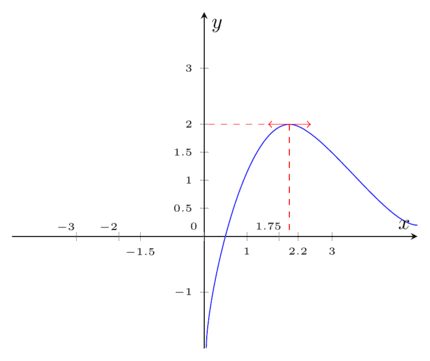
Cette figure représente la courbe d'une fonction \( C_g \) avec une tangente horizontale au point \( x = 2 \). La courbe est tracée en bleu et la tangente horizontale en rouge. La tangente horizontale, qui est parallèle à l'axe des abscisses, indique que le nombre dérivé de la fonction en ce point est nul. Cela signifie que la pente de la courbe en \( x = 2 \) est zéro. La présence de cette tangente horizontale suggère que le point de tangence est un point critique, où la courbe peut atteindre un maximum, un minimum ou un point d'inflexion. Des lignes pointillées rouges sont également utilisées pour montrer les projections de ce point critique sur les axes \( x \) et \( y \).