A Narcissistic number or otherwise known as a pluperfect digital invariant (PPDI) is a number that is equal to the sum of its digits each raised to the power of the number of its digits, it sort of loves itself (its digits), it is also called Armstrong number
The following numbers, in base 10 (Decimal) are Narcissistic: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 153, 370, 371, 407, 1634, 8208, 9474, 54748, 92727, 93084, 548834, ... There are Narcissistic numbers in all other Numeric bases
The algorithms to find Armstrong numbers are very simple
Python
The following Python code will find the Narcissistic numbers in base 10
n=10
while 1:
n += 1
sum = 0
n_digits = len(str(n))
for digit in str(n):
sum += int(digit)**n_digits
if sum == n:
print(n, "is armstrong")
Java
import java.util.Scanner;
public class ArmstrongNumber {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
System.out.println("Enter the number: ");
int num = in.nextInt();
double sum = requiredSum(num);
if (num == sum) {
System.out.println("Armstrong Number");
}
else {
System.out.println("Not an Armstrong Number");
}
}
public static int noOfDigits(int num) {
int i;
for (i = 0; num > 0; i++) {
num /= 10;
}
return i;
}
public static double requiredSum(int num) {
int i = noOfDigits(num);
double sum = 0;
while (num > 0) {
int digit = num % 10;
num /= 10;
sum += Math.pow(digit, i);
}
return sum;
}
}
C#
using System;
public class Program
{
public static void Main()
{
Console.WriteLine("Enter the number:");
int value = int.Parse(Console.ReadLine());
if (value == RequiredSum(value))
{
Console.WriteLine("Armstrong Number");
}
else
{
Console.WriteLine("Not an Armstrong Number");
}
}
private static int CountDigits(int num)
{
int i = 0;
for (;num > 0; ++i) num /= 10;
return i;
}
private static int RequiredSum(int num)
{
int count = CountDigits(num);
int sum = 0;
while (num > 0)
{
sum += (int)Math.Pow(num % 10, count);
num /= 10;
}
return sum;
}
}
C
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
int getNumberOfDigits(int n);
bool isArmstrongNumber(int candidate);
int main()
{
int userNumber = 0;
printf("Enter a number to verify if it is an Armstrong number: ");
scanf("%d", &userNumber);
printf("Is %d an Armstrong number?: %s\n", userNumber, isArmstrongNumber(userNumber) ? "true" : "false");
return 0;
}
bool isArmstrongNumber(int candidate)
{
int numberOfDigits = getNumberOfDigits(candidate);
int sum = 0;
for(int i = candidate; i != 0; i /= 10)
{
int num = i % 10;
int n = 1;
for(int j = 0; j < numberOfDigits; j++)
{
n *= num;
}
sum += n;
}
return sum == candidate;
}
int getNumberOfDigits(int n)
{
int sum = 0;
while(n != 0)
{
n /= 10;
++sum;
}
return sum;
}
C++
The following C++ program determines whether the Integer entered is a Narcissistic / Armstrong number or not.
#include <iostream>
#include <cmath>
bool isNarcissistic(long n) {
std::string s = std::to_string(n); // creating a string copy of n
unsigned short l = s.length(); // getting the length of n
unsigned short i = 0; long sum = 0; unsigned short base; // i will be used for iteration, sum is the sum of all of the digits to the power of the length of the number, and the base is the nth digit of n
while(i<l) { // iterating over every digit of n
base = s.at(i)-48; // initializing the base of the number and subtracting 48 because the ascii for 0 is 48 and the ascii for 9 is 57 so if we subtract 48 it will give a integer version of that character.
sum += pow(base,l); // adding base^length to the sum variable
i++; // incrementing the iterator
}
return (n==sum) ? true : false; // if the n is equal to the sum return true, else, return false
}
int main() {
unsigned int candidate; // declaring the candidate variable
std::cout << "Enter a number to verify whether or not it is a narcissistic number: "; // printing the prompt to gather the input for the candidate variable.
std::cin >> candidate; // taking the user's input
std::cout << (std::string)((isNarcissistic(candidate)) ? "Yes" : "No") << std::endl; // printing "Yes" if it is an armstrong number and printing "No" if it isn't
return 0; // returning 0 for a success
}
1.23K views
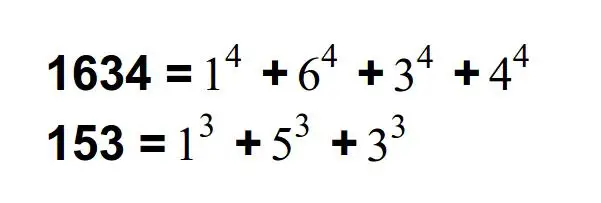



















0 Comments, latest