The Fascinating World of Amicable Numbers: History, Discoveries, and Insights

Thābit ibn Qurra ثابت بن قرة

In the rich tapestry of mathematical history, Thābit ibn Qurra ثابت بن قرة stands as a towering figure whose contributions continue to inspire awe and admiration. A polymath of the Islamic Golden Age, Thābit ibn Qurra delved into various branches of mathematics, astronomy, and medicine, leaving an indelible mark on each. Among his many achievements, Thābit ibn Qurra is credited with introducing the concept of amicable numbers to the world, providing one of the earliest known formulas for generating these fascinating pairs. His pioneering work not only illuminated the realm of number theory but also paved the way for future mathematicians to explore the intricate patterns and relationships hidden within the numerical landscape.

Amicable Numbers

Amicable numbers are two different numbers so related that the sum of the proper divisors of one of the numbers is equal to the other. A proper divisor of a number is a positive integer divisor other than the number itself. For example, the proper divisors of 6 are 1, 2, and 3.

Two numbers are called Amicable (or friendly) if each equals to the sum of the proper divisors of the other. For example, the proper divisors of number 220 are 1, 2, 4, 5, 10, 11, 20, 22, 44, 55, and 110. The proper divisors of number 284 are 1, 2, 4, 71, and 142.

If we represent an amicable pair (AP) by (m, n) and sum of the proper divisors of m and n by σ(m) and σ(n) respectively, then (220, 284) form an amicable pair since σ(m) = σ(220) = 1+ 2+ 4+ 5+ 10+ 11+ 20+ 22+ 44+ 55+ 110 = 284 = n, and σ(n) = σ(284) = 1+ 2+ 4+ 71+ 142 = 220 = m

Thābit ibn Qurra's Formula for Amicable Numbers

For positive numbers n superior to 1, The amicable number pairs take the values and 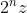where

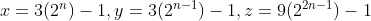
This is a good example of using Thābit ibn Qurra's formula to find amicable numbers. Here's a detailed analysis of the example:

For the value n = 2, we obtain x = 11, y = 5, z = 71, which are prime numbers. Now, using the formula we find n= 220 and m=284 which make an amicable paire

However, this method does not generate all amicable numbers. More sophisticated algorithms are needed to generate all possible amicable numbers.

In 1636, Pierre de Fermat discovered another pair of amicable numbers (17296, 18416). Later Descartes gave the third pair of amicable numbers i.e. (9363584, 9437056). In the 18th century, Euler drew up a list of 64 amicable pairs. B.N.I. Paganini, a 16 years old Italian, startled the mathematical world in 1866 by announcing that the numbers 1184 and 1210 were friendly. It was the second-lowest pair and had been completely overlooked until then. Until 28 Sept 2007, about 11,994,387 pairs of amicable numbers are known.

(17296, 18416) also form an amicable pair.